Mathematical maps

Category theorist studies the structure of the abstract

By Jennifer Tidball

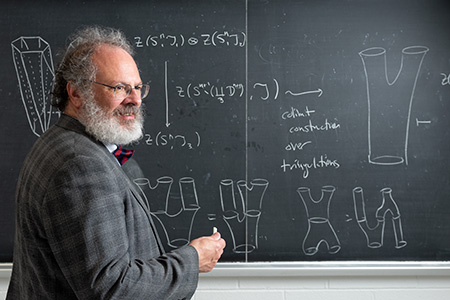In the mathematical research frontier, David Yetter considers himself a fur trapper of sorts.

“The fur trappers used to be the ones who would go out on the frontier, explore uninhabited areas and bring back news of what was out there,” said Yetter, Kansas State University distinguished professor of mathematics in the College of Arts and Sciences. “A lot of my work has, like the old fur trappers, been in areas where no one else was working yet and afterward other mathematicians discovered that things I found first were far more important than I could ever have guessed.”

Yetter primarily studies category theory, which is an abstract form of mathematics focused on mathematical structure. It has applications to other areas of mathematics and to computer science and theoretical physics.

“The key insight of category theory is that maps between mathematical objects are as important as the mathematical objects themselves,” Yetter said.

Yetter has published papers in knot theory, geometry, graph theory, logic and functional analysis, all either applying category theory to those areas or solving problems that only came to light from applying category theory to another area of mathematics. Some of his current work involves applying category theory to geometric problems. His research relates to quantum field theory as well.

“It turns out that category theory is very closely related to the way mathematicians try to formalize quantum field theory,” Yetter said. “In topological quantum field theory, the key idea is to cut a geometric shape into simple pieces and the assembly of those pieces has an algebraic structure that is governed by some sort of category.”

Several topological quantum field theories are named for him: the Yetter model, which can be defined in any dimension, and the Crane-Yetter model, a fourdimensional topological quantum field theory that he developed with Louis Crane, K-State professor emeritus of mathematics. Modifications of the Crane-Yetter model are the basis for the Barrett-Crane and EPRL models of quantum gravity. Yetter continues to collaborate with Crane on applying category theory to fundamental physics.

In addition to his own research, Yetter is the co-director of K-State’s mathematics Research Experiences for Undergraduates program called SUMaR, or the Summer Undergraduate Mathematics Research program. The National Science Foundation funds the program, which offers undergraduates across the country the opportunity to visit K-State and work on projects in knot theory and other topics.

Yetter came to K-State in 1991. Throughout his career, his work has been supported by more than $1.5 million in NSF research grants. He has published 47 journal or refereed proceedings articles and has written 11 widely distributed unpublished manuscripts as well as the monograph “Functorial Knot Theory.”

He has held research positions with the Institute for Advanced Study, McGill University, the Groupe Interuniversitaire en Études Catégoriques in Montreal and the Mathematical Sciences Research Institute. He has been a visiting fellow in mathematics at Macquarie University in Australia and a visiting researcher at the University of Sheffield in the United Kingdom.